Aufgabe 170
Die 4 Wiesen sollen eingezäunt werden?
Wie viel m Zaun braucht man, wenn zwischen
benachbarten Wiesen nur ein Zaun gezogen wird?
 Es sind m
Es sind m
Wie löse ich Matheaufgaben?
Flächenberechnungen
Sie sehen ein gelbes Eingabefeld und die
Schalter: Prüfen und Lösung.
Tragen Sie Ihr Ergebnis ein, prüfen Sie es
oder starten Sie eine Lösung.
Aufgabe 168 Ein rechteckiges Grundstück ist 861 m2 groß und hat eine Straßenfront von 21 m. Das Nachbargrund- stück hat eine Fläche von 720 m2 und eine Straßenfront von 18 m. Um wie viel m ist das eine Grundstück länger als das andere? Der Unterschied ist m
Aufgabe 169 Ein Grundstück von 400 m2 hat die Form eines Trapezes. Die Straßenfront ist 20 m lang, die gegenüberliegende Seite 12 m. Wie tief ist das Grundstück?
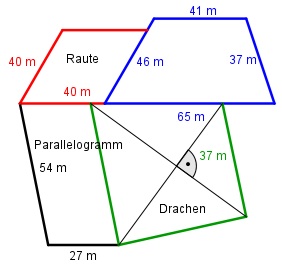
Aufgabe 170 Die 4 Wiesen sollen eingezäunt werden? Wie viel m Zaun braucht man, wenn zwischen benachbarten Wiesen nur ein Zaun gezogen wird?
Es sind m
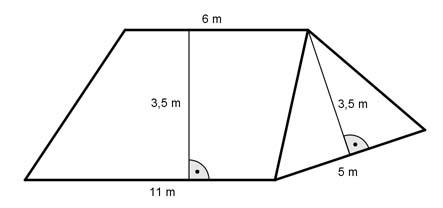
Aufgabe 171 Wie groß ist die Dachfläche A? Wie lang ist die Dachrinne?
Aufgabe 172 Die Kreisbahn der Erde um die Sonne hat einen Radius von 150 Mio km. Wie groß ist deren Länge? Mit welcher Geschwindigkeit bewegt sich die Erde, wenn sie 365 Tage für eine Umrundung braucht? Mit km/h
Aufgabe 173 Ein Mast hat einen Umfang von 41,8 cm. Wie lang muss ein Stift sein, der mittig eingesetzt wird und beidseitig 1 cm übersteht?
Aufgabe 174 Ein Ausschnitt eines kreisrunden Beetes (r = 5 m, Mittelpunktswinkel 150°) wird bepflanzt. Wie groß ist seine Fläche? A = m2 Wie viele Pflanzen braucht man, wenn mit 9 Pflanzen pro m2 gerechnet wird?
Aufgabe 175 Ein Platz 180 m x 105 m soll rundum mit Bäumen im Abstand von 15 m bepflanzt werden. An den Ecken soll jeweils ein Baum stehen. Wie viel Bäume braucht man?
Aufgabe 176 Eine Baugrube 15 m x 8 m soll mit Absperrband im Abstand von 2 m gesichert werden. Wie lang muss das Band sein? l = m
Aufgabe 177 In einer Innenstadt soll eine Fläche 55 m x 39 m als Parkplatz für 162 PkW genutzt werden. Die Zufahrten nehmen 450 m2 in Anspruch. Wie viel Stellfläche ergibt sich pro Pkw?
Aufgabe 178 Wie lang muss ein Zaun sein, der eine kreisrunde Fläche von 254,5 m2 begrenzen soll? l = m
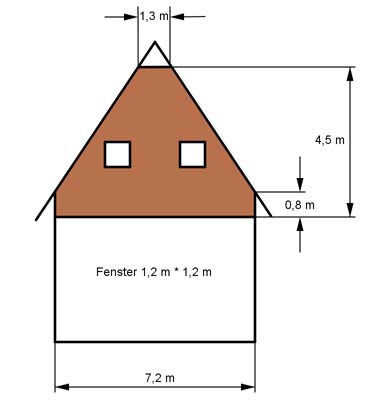
Aufgabe 179 Wie viel m2 Holz braucht man für die Verschalung, wenn mit 20% Verschnitt gerechnet wird?
Aufgabe 180 Um ein kreisförmiges Blumenbeet mit einem Radius von 2 m ist ein 3 m breiter Rasenstreifen angelegt. Wie groß ist die Fläche A des Beetes? A = m2 Wie groß ist die Rasenfläche?
Aufgabe 181 Eine Gemeinde will einen Platz mit 10 000 Blumen bepflanzen und zwar mit 50 Blumen pro m2. Ein Gärtner will dafür eine kreisrunde, ein anderer eine quadratische Fläche anlegen. Um die Fläche soll jeweils ein 1 m breiter Weg verlaufen. Wie groß ist die Wegfläche um den Kreis? Um das Quadrat?
Aufgabe 182 Der Sportplatz wird erneuert. Die 6 m breite Laufbahn kostet 45 € pro m2, der Rasen 15 € pro m2, das Verlegen weitere 3,75 € pro m2. Wie hoch ist der Gesamtpreis?
Er beträgt €
Aufgabe 183 Die Fahrbahn eines Kreisverkehrs ist innen 200 m und außen 300 m lang. Wie groß ist ihre Fläche?
Aufgabe 184 Die Einzäunung einer Fläche von 700 m2 kostet 80 € pro laufenden Meter. Wie viel kostet der Zaun, wenn die Fläche rechteckig ist und 35 m lang? Kosten = € Wie viel kostet er, wenn die Fläche quadratisch ist?
Aufgabe 185 In einem Zelt haben 2 400 Personen Platz. Welchen Durchmesser muss das Zelt haben, wenn auf einem m2 maximal 3 Personen stehen sollen?
Aufgabe 186 Das Vorderrad eines Traktors hat einen Durchmesser von 95 cm, das Hinterrad einen von 155 cm. Wie weit hat sich der Traktor bei einer Umdrehung des Vorderrades bewegt? Es sind cm Das Vorderrad macht 60 Umdrehungen, wie viele macht das Hinterrad?
Aufgabe 187 34 Kinder fassen sich an den Händen (von Hand zu Hand 1,3 m), um einen Baumstamm zu umfassen. Welchen Durchmesser hat er?
Aufgabe 188 Der Sportplatz soll erneuert werden. 2 Angebote liegen vor. Angebot 1: Angebot 2: Kunstrasen 34 €/m2 45,60 €/m2 Erdarbeiten 16 €/m2 18,75 €/m2 Rasen verlegen 4,45 €/m2 6,25 €/m2 Laufbahn 42 €/m2 88 €/m2 Arbeitskosten 6,30 €/m2 Erdarbeiten 15,80 €/m2 ohne mit MWSt von 19% Wie teuer ist das günstigere Angebot?
Es sind €
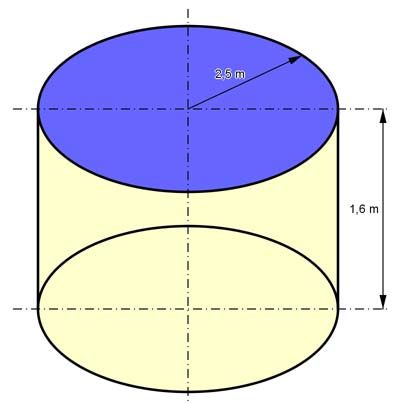
Aufgabe 189 Das Becken wird neu gefliest. Wie viel m2 Fliesen braucht man? Ein m2 Fliesen kostet 24,55 €, das Verlegen 8 €/m2. Wie hoch sind die Kosten einschließlich Mehrwertsteuer, wenn noch 10% Prozent für Verschnitt berücksichtigt werden?
Aufgabe 190 Ein Gartenplaner macht den dargestellten Vorschlag. Rasen = grüne Flächen Blumenbeete = gelbe Flächen Verbindungswege von außen nach innen = Rechtecke
Wie viel Platz braucht er dafür? Er braucht m3 Wie viel Steine braucht man für die Wege und Umrandung bei 55 Steinen/m2? Wie groß ist die Blumenbepflanzung? Wie viel g Grassamen braucht man bei benötigten 15 g/m2? Der Teich in der Mitte ist 60 cm tief und ist bis 5 cm unter der Oberkante gefüllt. Wie viel m3 Wasser sind nötig?
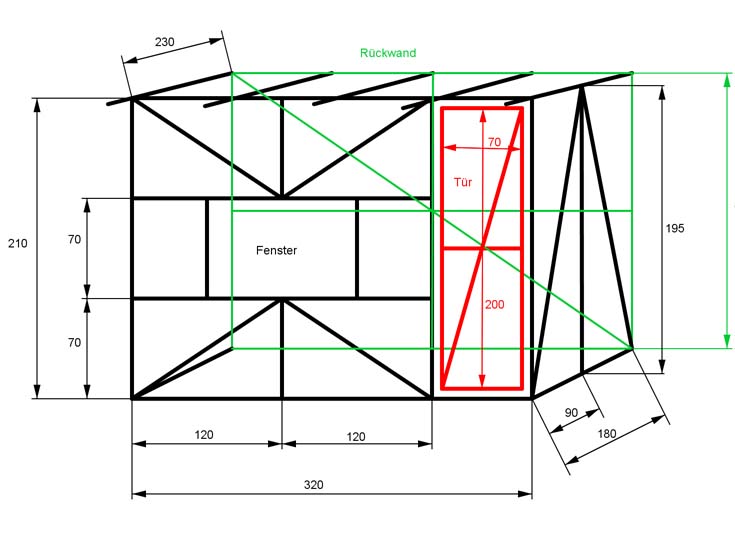
Aufgabe 191 Sie wollen das Gartenhaus bauen. Wie viel Meter Holzbalken brauchen Sie, wenn die Dicke vernachlässigt und mit einem Verschnitt von 8% gerechnet werden soll? Wieviel kostet das Holz, wenn 8 cm * 8 cm Balken verwendet werden und der m3 218,65 € kostet? Auf das 3 cm dicke Dach soll Teerpappe verlegt werden. Wie teuer wird es bei einem Verschnitt von 5%, wenn das Holz 228,75 €/m3 kostet und die Pappe 0,68 €/m2? Für die Außenverkleidung verwenden Sie Bretter, die pro m2 9,96 € kosten. Wie teuer ist die Verkleidung bei 5% Verschnitt?
Aufgabe 192 Wie viel m wäre der Erdumfang länger, wenn der Erdradius (6 370 km) um 1 m größer wäre? Es wären m Um wie viel m müsste der Erdradius vergrößert werden, wenn der Umfang um 1 km größer werden soll?
Aufgabe 193 Das Hinterrad eines Fahrrades hat einen Durch- messer von 80 cm. Das Kettenrad vorne hat doppelt so viel Zähne wie hinten. Wie oft muss ein Pedal getreten werden, um 1 km zurückzulegen? Welche Geschwindigkeit erzielt man, wenn pro s ein Pedaltritt erfolgt?
Aufgabe 194 Berechnen Sie die Kontrollabstände AD, AE, CE, AG und CH der Bohrschablone.
CE = mm
Aufgabe 195 Sie sollen aus einem 58 cm langen Draht ein Rechteckbiegen, dessen eine Seite 6 cm länger ist als die andere. Wie lang ist die kürzere Seite?
Aufgabe 196 Ein rechteckiger Platz mit einer Diagonalen von 115 m und einer Fläche von 6 000 m2 wird umzäunt. Welche Holzmenge ist erforderlich, wenn für den laufenden Meter 0,25 m2 Holz gebraucht werden? Holzmenge = m3 Wie groß ist die längere Rechteckseite?
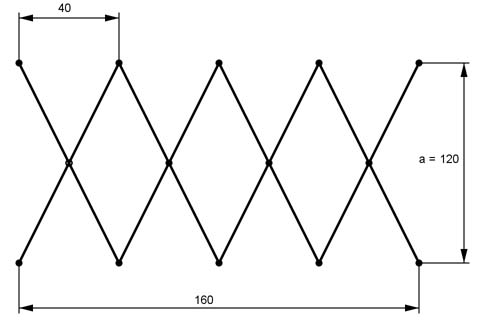
Aufgabe 197 Um welchen Betrag verlängert sich das Gelenk- system, wenn a auf ein Drittel verkürzt wird?
Aufgabe 198 Ein rechteckiger Bilderrahmen mit den äußeren Abmessungen 64 cm * 92 cm ist aus Holzleisten zusammengesetzt. An den Ecken ist unter 45° ein 3,54 cm langer Gehrungsschnitt nötig. Wie groß sind die innere Rahmenfläche A und die Breite b der Leisten? b = cm
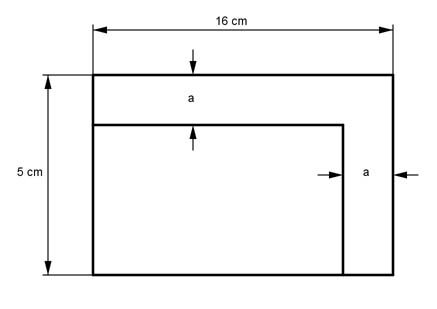
Aufgabe 199 Wie groß ist a, wenn sich die Fläche des Rechtecks um ein Drittel verringern soll?
Aufgabe 200 Aus einem quadratischen Blech mit der Seitenlänge 6 cm solleine Raute ausgeschnitten werden, dessen eine Diagonale so groß ist wie die Diagonale des Quadrates, die andere halb so lang. Wie groß sind der Blechverlust V und die Seitenlänge b der Raute? V = cm2
Aufgabe 201 Wie groß ist der Schnittverlust für 100 Bleche, wenn das fertige Teil aus einem 32 mm * 46 mm großen Blech hergestellt wird?
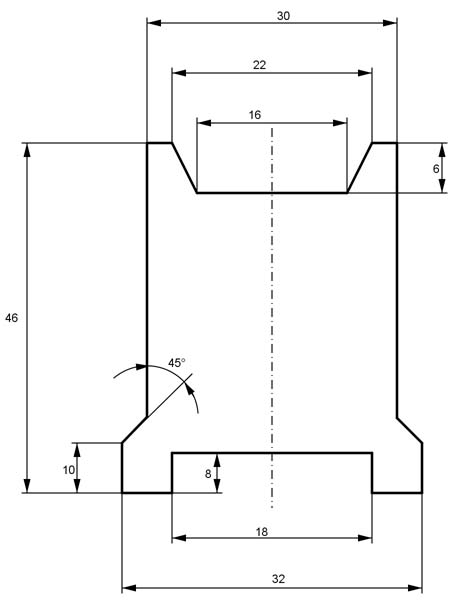
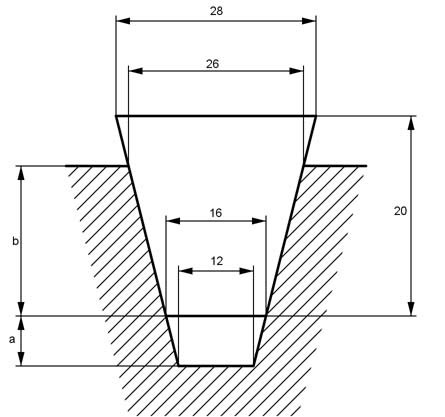
Aufgabe 202 Wie groß sind der Querschnitt A des Kanals und die Länge a?
A = m2
Aufgabe 203 Wie groß sind a und b und der in der Nut freibleibende Querschnitt A?
Aufgabe 204 Ein Brunnen hat als Grundfläche ein regelmäßiges Achteck von 15,4 m2. Wie groß ist eine Seite s des Achtecks? s = m
Aufgabe 205 Eine regelmäßige Sechsecksäule mit einer Seiten- länge von 32 cm steht auf einem zylindrischen Sockel. Wie groß ist dessen Durchmesser d, wenn er beidseits 6 cm über die längere Sechseckdiagonale hinausragt?
Aufgabe 206 Der Boden eines Gefäßes wird von einem regelmäßigenZehneck mit einem Umfang von 20 cm gebildet. Wie groß ist dessen Umkreisradius r? r = cm
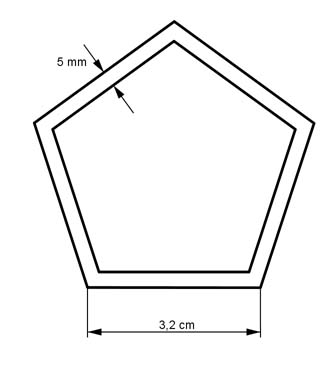
Aufgabe 207 Das zu groß geratene Blech (regelmäßiges Fünfeck) wird sobearbeitet, dass parallel zu den Seiten Streifen von 5 mm wegfallen. Wie groß sind die Fläche A und die Seitenlänge s des neuen Fünfecks?
Aufgabe 208 Ein Dreikantstahl (A = 8 cm2) soll parallel zu einer Seite auf 5 cm2 abgefräst werden. Welche Frästiefe a muss gewählt werden, wenn ein regelmäßiges Dreieck erhalten bleiben soll? a = cm
Aufgabe 209 Die Grundflächen eines dreistöckigen Pavillons sind regelmäßige Sechsecke. Wie groß sind die Seiten der nächsten Etagen, wenn die Grundseite 3 m beträgt und die Sechsecke jeweils 0,5 m zurückspringen?
Aufgabe 210 Der Umfang einer Weide in Form eines regelmäßigen Zehn ecks beträgt 45 m. Wie groß ist ihre Fläche A? A = m2
Aufgabe 211 Ein Museum hat ein Seitenfenster in Form eines regelmäßigen Sechsecks. Seine Randeinfassung besteht aus Holzleisten mit einer Breite von 5 cm und einem äußeren Umfang von 3 m. Wie groß ist die Fläche A für den Lichteinfall?
Aufgabe 212 Aus einem quadratischen Blech mit einer Seiten- länge von 16 cm soll an den Ecken ein Achteck geschnitten werden. Wie groß ist dessen Fläche A? A = cm2
Aufgabe 213 Aus 12 regelmäßigen Sechseckblechen sollen 12 Dreiecke mitgrößtmöglicher Seitenlänge entstehen. Wie groß ist der Schnittverlust V, wenn eine Sechseckseite 14,5 cm lang ist?
Aufgabe 214 Als Stützen für einen Vorbau sind regelmäßige Zehnecksäulen vorgesehen. Wie groß ist eine Seite a der Säule, wenn der Abstand der parallelen Seiten 45 cm sein muss? s = cm
Aufgabe 215 Aus einem runden Stamm mit einem Durchmesser von 56 cm soll ein Sechseck mit geringstmöglichem Verlust geschnitten werden. Wie groß ist der Umfang U des Sechsecks?
Aufgabe 216 Ein Kupferdraht von 2 mm2 soll durch einen mit dreifachem Querschnitt ersetzt werden. Welchen Durchmesser d hat der neue Draht? d = mm
Aufgabe 217 Das Rad eines Pkw muss sich 400 mal drehen, damit es 1 km zurücklegt. Welchen Durchmesser d hat es?
Aufgabe 218 Ein Autoreifen hat einen Außendurchmesser von 92 cm. Wie viel Umdrehungen muss er auf einen km mehr machen, wenn er auf 88 cm zurückgegangen ist? n = Umdrehungen
Aufgabe 219 Aus einem Blech von 35 cm Breite soll ein Rohr mit einer lichten Weite von 10 cm gebogen werden. Um wie viel cm steht der Rand über?
Aufgabe 220 Ein Rohr soll stündlich 500 m3 Wasser mit einer Geschwindigkeit von 0,11 m/s fördern. Wie groß muss der Innendurchmesser d des Rohres sein? d = m
Aufgabe 221 Ein Rohr soll bei gleichem Querschnitt 2 Rohre von 24 cm und 38 cm Durchmesser ersetzen. Wie groß muss sein Durchmesser d sein?
Aufgabe 222 Ein Fahrzeug hat Vorderräder mit einem Durch- messer von 32 cm und Hinterräder mit einem von 38 cm. Wie viel Umdrehungen müssen die Vorderräder auf einer Strecke von 8,4 km mehr machen? n = Umdrehungen
Aufgabe 223 Eine Welle hat einen Umfang von 21 cm. Wie groß ist ihre Fläche A und ihr neuer Umfang U, nachdem 0,5 cm abgedreht wurden?
Aufgabe 224 Wie groß ist der Schnittverlust V?
V = mm2
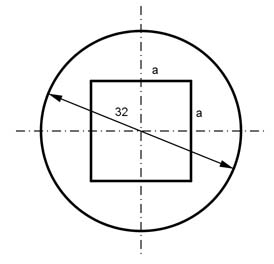
Aufgabe 225 Wie groß ist die Seite a der quadratischen Aussparung, wenn sich der Querschnitt der Welle halbieren soll?
Aufgabe 226 Ein Rohr hat eine Wanddicke von 14 mm und einen lichtenDurchmesser von 75 mm. Wie groß ist die Materialfläche A? A = mm2
Aufgabe 227 Ein kreisringförmiger gemauerter Brunnen hat einen äußerenUmfang von 9,5 m und einen inneren von 7,2 m. Wie groß ist die Fläche A des Mauerwerks?
Aufgabe 228 Eine Welle von 84 mm soll auf die Hälfte seiner Fläche aufgebohrt werden. Wie groß ist der Bohrungsdurchmesser d? d = mm
Aufgabe 229 Über einen Vierkantstahl mit einer Seitenlänge von 31 mm soll eine zylindrische Hülse mit einem äußeren Umfang von 150 mm geschoben werden. Wie groß ist die Wanddicke a der Hülse?
Aufgabe 230 Wie groß ist die Fläche A der Schelle? Die Laschen seien Rechtecke.
A = mm2
Aufgabe 231 Aus einem Blech von 1,5 m Länge und 3 cm Breite sollen Ringemit 24 mm Außen- und 12 mm Innen- durchmesser ausgestanzt werden. Wie groß ist der Abfall A, wenn zwischen den Ringen und am Anfang und Ende ein Abstand von 3 mm eingehalten werden soll?
Aufgabe 232 Wie groß ist die gestreckte Länge l des Rohrbogens?
l = m
Aufgabe 233 Wie groß ist der Durchflussquerschnitt A des Kanalrohrs?
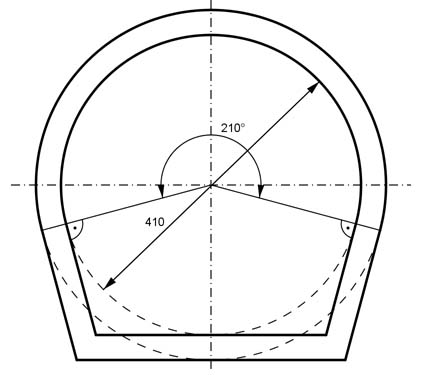
Aufgabe 234 Wie groß ist der Materialbedarf A für die 4 Lamellen?
A = mm2
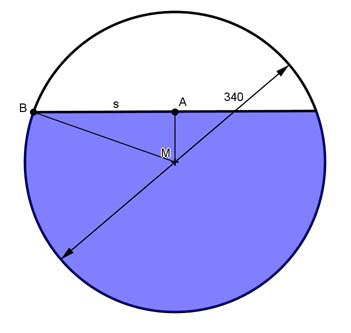
Aufgabe 235 In welcher Höhe h steht das Wasser in der Tonne, wenn sie zu 2/3 gefüllt ist, und wie lang ist die Sehne s?
Aufgabe 236 Die Welle ist oben auf eine Breite von 20 mm abgefräst. Berechnen Sie die Einstelltiefe t des Fräsers.
t = mm
Aufgabe 237 Aus einer Scheibe mit einem Durchmesser von 67 mm soll ein Kreissektor so ausgeschnitten werden, dass der Umfang auf einer Bogenlänge von 51 mm unterbrochen wird. Wie groß ist der Mittelpunktswinkel α?
Aufgabe 238 Berechnen Sie das Maß a des dargestellten Bremsklotzes.
a = mm
Aufgabe 239 Eine Bremstrommel hat einen Durchmesser von 250 mm. Das Bremsband berührt den Umfang der Trommel auf einer Länge von 540 mm. Wie groß ist der Umschlingungswinkel α?
Aufgabe 240 Die dargestellte Lehre ist aus einer Scheibe von 76 mm Durchmesser herausgearbeitet worden. Wie groß ist der Blechabfall A?
A = mm2
zurück