Trigonometrie

Wie löse ich Matheaufgaben?

Trigonometrie

Sie sehen ein gelbes Eingabefeld und die
Schalter: Prüfen und Lösung.

Tragen Sie Ihr Ergebnis ein, prüfen Sie es
oder starten Sie eine Lösung.

Aufgabe 133

Berechnen Sie die Seite b, wenn a = 7,8 cm, 
c = 9,6 cm und γ = 68°.

Aufgabe 134 Berechnen Sie die Seite c, wenn b = 2,4 m, α = 43° und β = 64°. c = m

Aufgabe 135 Berechnen Sie die Seite a, wenn b = 62,8 cm, α = 65° und γ = 48°.

Aufgabe 136 Berechnen Sie die Seite b, wenn a = 322,6 m, c = 283,7 m und γ = 27°. kürzere Seite = m

Aufgabe 137 Berechnen Sie den Winkel α, wenn a = 14,3 m, b = 26 m und γ = 82,1°.

Aufgabe 138 Berechnen Sie die Fläche A des Parallelogramms. A = cm²

Aufgabe 139 Berechnen Sie den Winkel α, wenn a = 27 m, c = 38 m und β = 124°.

Aufgabe 140 Berechnen Sie die Fläche A eines Dreiecks, wenn a = 45 m, b = 296 m und c = 325 m. A = m²

Aufgabe 141 Berechnen Sie den Umkreisradius r_a und den Inkreisradius r_i eines Dreiecks, wenn a = 32,1 m, b = 13,2 m und c = 39,4 m.

Aufgabe 142 Berechnen Sie die Länge der Diagonalen f, wenn a = 3,9 cm, b = 2,1 cm und α = 47°. f = cm

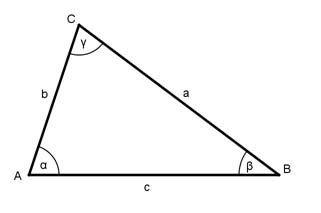
Aufgabe 143 Berechnen Sie den Winkel γ, wenn b = 4,5 cm, c = 5 cmund h_c = 3 cm.

Aufgabe 144 Berechnen Sie die Seite a, wenn ha = 25,3 m, α = 98,8° und β = 34,2°. a = cm

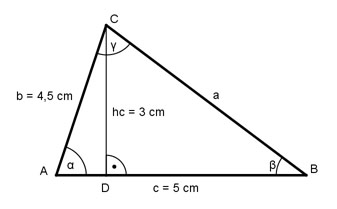
Aufgabe 145 Berechnen Sie den Winkel α, wenn a = 55,6 m, c = 66 m und die Seitenhalbierende s_c = 32,7 m.

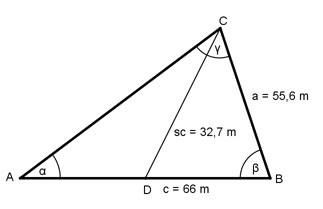
Aufgabe 146 Wie lang ist die kleinere der fehlenden Dreieckseiten, wenn b = 6,25 m, h_b = 5,12 m und s_b = 5,57 m. Sie ist m lang.

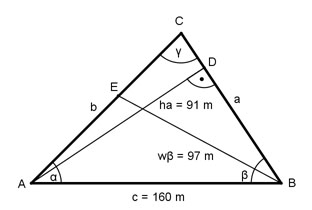
Aufgabe 147 Berechnen Sie die Seite b, wenn c = 160 m, h_a = 91 m und die Winkelhalbierende w_β = 97 m.

Aufgabe 148 Berechnen Sie die Seite b, wenn h_c = 4 cm, w_γ = 4,4 cm und s_c = 5,3 cm. b = cm

Aufgabe 149 Berechnen Sie den Winkel α, wenn sich die Seiten a, b und c wie 3 : 5 : 7 verhalten.

Aufgabe 150 Berechnen Sie den Winkel β, wenn b = 42,5 m, γ = 85°40' und a und c sich wie 5 : 8 verhalten. β = °

Aufgabe 151 Wie groß ist die Fläche A des Parallelogramms?

Aufgabe 152 Wie groß sind die Fläche A und die Seite b des gleichschenkligen Trapezes? A = m²

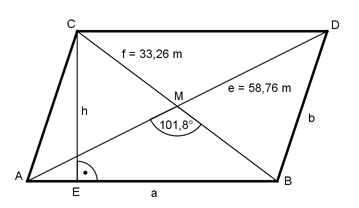
Aufgabe 153 Wie groß sind die Diagonalen e und f des Trapezes?

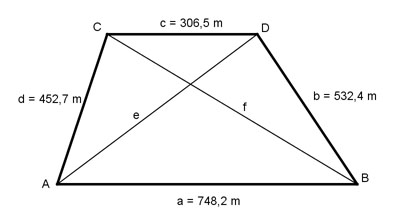
Aufgabe 154 Wie groß sind die Seite c und die Diagonale f des Trapezes? c = m

Aufgabe 155 Wie groß ist die Seite c des Sehnenvierecks?

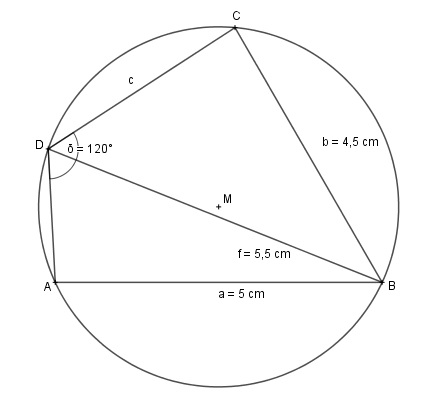
Aufgabe 156 Wie groß ist die Seite d des Sehnenvierecks? d = mm

Aufgabe 157 Wie groß ist der Winkel δ des Vierecks?

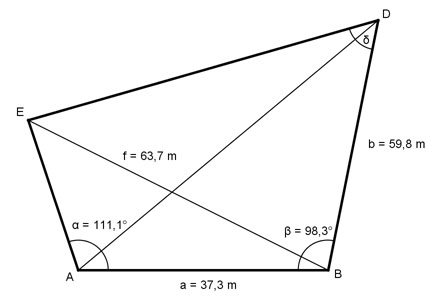
Aufgabe 158 Wie groß ist die Diagonale e des Drachenvierecks? e = cm

Aufgabe 159 Wie groß ist die Diagonale f des Drachenvierecks?

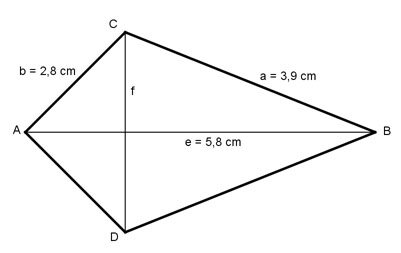
Aufgabe 160 Wie groß ist die Diagonale f des Drachenvierecks? f = cm

Aufgabe 161 Wie groß ist die Seite b des Drachenvierecks?

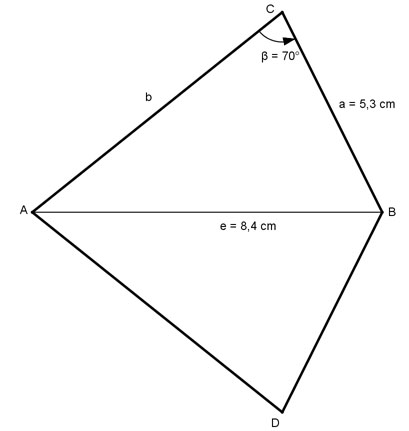
Aufgabe 162 Wie groß ist die Diagonale f des Sehnenvierecks? f = cm

Aufgabe 163 Wie groß ist die Diagonale f des Sehnenvierecks?

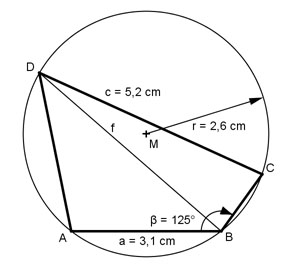
Aufgabe 164 Die Mittelpunkte zweier Kreise mit den Radien r₁ = 6 cm und r₂ = 4 cm liegen 8 cm auseinander. Wie groß ist die gemeinsame Sehne s? s = cm

Aufgabe 165 Wie groß ist die Seite c des gleichschenkligen Trapezes?

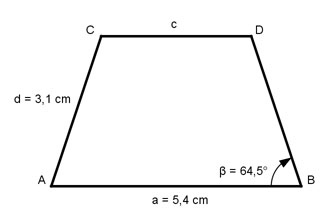
Aufgabe 166 Wie groß ist die Seite a des gleichschenkligen Trapezes? a = cm

Aufgabe 167 Wie groß ist die Seite a des gleichschenkligen Trapezes?

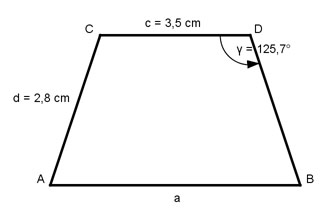
Aufgabe 168 Wie groß ist die Diagonale e des gleichschenkligen Trapezes? e = km

Aufgabe 169 Wie groß sind die Oberfläche O und das Volumen V einer Dreieckspyramide mit 10 cm langen Seiten- kanten, wenn die Seiten der Grundfläche a = 5 cm, b = 7 cm und c = 8 cm lang sind? Wie groß ist der Winkel α, den die Seitenkanten mit der Grundfläche bilden? Wie groß ist der Winkel β, den die Grundfläche mit der Seitenfläche über a bildet?

Aufgabe 170 Aus einem Kreisausschnitt mit dem Radius r = 15 cm und dem Mittelpunktswinkel α = 105° ist ein Kegel gebogen worden. Wie groß ist dessen Volumen V? V = cm³

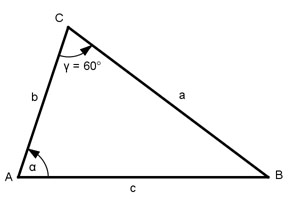
Aufgabe 171 Wie groß sind die Seite c und der Winkel α, wenn a + b = 52 cm, γ = 60° , A = 160 * √3 cm³ und a > b sein soll?

Aufgabe 172 Die Seitenfläche und die Grundfläche einer regelmäßigen geraden dreiseitigen Pyramide verhalten sich wie 2 : 1. Berechnen Sie den Neigungswinkel α einer Seitenfläche gegen die Grundfläche. α = °

Aufgabe 173 Durch die Grundseite a = 4 cm eines geraden regelmäßigen dreiseitigen Prismas verläuft eine Ebene, die um 50,7° geneigt ist. Wie groß ist das Volumen V der abgeschnittenen Pyramide?

Aufgabe 174 Eine gerade regelmäßige fünfseitige Pyramide hat die Grundseite a = 10 cm und Seitenkanten s = 13 cm. Wie groß sind der Winkel α zwischen Grundseite und Seitenkante und der Winkel δ zwischen zwei Seitenflächen? α = °

Aufgabe 175 Ein gerades dreiseitiges Prisma, dessen Höhe > 56 cm ist, hat als Grundfläche ein Dreieck mit den Seiten a = 33 cm, b = 21 cm und c = 45 cm. Eine Ebene, die durch C geht, schneidet die Seitenkante über A in einer Höhe von 28 cm, die über B in einer Höhe von 56 cm. Wie groß sind die größte Seite s dieses Schnitt- dreiecks und seine Fläche A?

Aufgabe 176 Ein gerades dreiseitiges Prisma hat ein Volumen von 400 cm³. Seine Grundfläche hat die Winkel α = 42,5° und β = 71,3°. Wie groß ist das Volumen V des umschriebenen Zylinders? V = cm³

Aufgabe 177 Ein schiefer Kegel hat eine längste Mantellinie von 30 cm, mit einem Neigungswinkel von 31,2°. Seine kürzeste hat einen Neigungswinkel von 82,4°. Wie groß ist das Volumen V des Kegels?

Aufgabe 178 Einem geraden Kegel mit dem Öffnungswinkel α = 31,6° ist eine Kugel mit dem Durchmesser d = 55,4 cm einbeschrieben. Wie groß ist das Volumen V des Kegels? V = dm³

Aufgabe 179 Berechnen Sie den Winkel α, den eine Raum- diagonale des Quaders mit einer Flächen- diagonale und den Schnittwinkel β, den zwei Raumdiagonalen miteinander bilden.

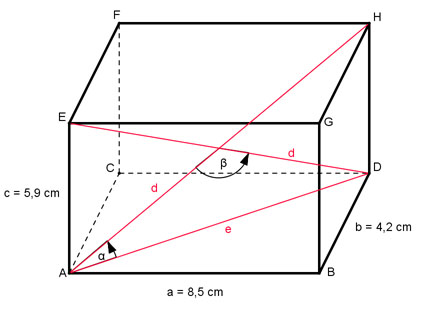
Aufgabe 180

Wie groß ist die Seite d?  



d =  cm

zurück