Volumen

Wie löse ich Matheaufgaben?

Volumen

Aufgabe 1 Welches Volumen V und welche Oberfläche O hat ein Würfel mit der Seitenlänge a = 3 cm?

Aufgabe 2

Welche Seitenlänge a hat ein Würfel 
a) mit dem Volumen V = 64 cm³?
b) mit der Oberfläche = 150 cm²?  

b) a =  cm

Aufgabe 3 Ein Prisma hat einen Umfang U der Grundfläche von 56,8 dm, eine Höhe h von 9,5 dm und eine Grundfläche G von 94,5 dm². Wie groß sind die Mantelfläche M und die Oberfläche O?

Aufgabe 4 Ein Prisma hat eine Grundfläche G von 63,8 cm², eine Höhe h von 22,5 cm und eine Mantelfläche M von 518,75 cm². Wie groß sind die Oberfläche O und der Umfang U der Grundfläche? U = cm

Aufgabe 5 Ein Prisma hat eine Oberfläche O von 54,63 cm², eine Mantelfläche M von 36,83 cm² und einen Umfang U der Grundfläche von 6,35 cm. Wie groß sind die Grundläche G und die Höhe h?

Aufgabe 6 Ein Prisma hat eine Oberfläche O von 1225 cm², eine Höhe h von 23 cm und einen Umfang U der Grundfläche von 42 cm. Wie groß sind die Grundläche G und die Mantelfläche M? M = cm²

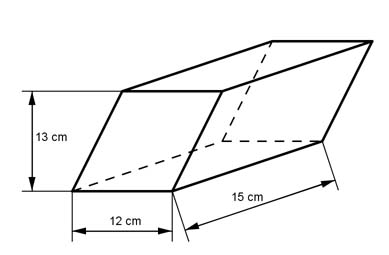
Aufgabe 7 Berechnen Sie das Volumen V des dargestellten Prismas.

Aufgabe 8 Berechnen Sie das Volumen V des dargestellten Prismas. V = cm³

Aufgabe 9 Berechnen Sie die Höhe h eines Prismas mit dem Volumen V = 180,7 dm³ und einer Grundfläche G = 27,8 dm².

Aufgabe 10

Berechnen Sie das Volumen V eines Prismas (Quaders) 
mit der Länge a = 4 cm, der Breite b = 3 cm und 
der Höhe h = 70 mm. 

V =  cm³

Aufgabe 11

Berechnen Sie das Volumen V eines Prismas (Quaders) 
mit der Länge a = 15 cm, der Breite b = 85 cm und 
der Höhe h = 9 dm.

Aufgabe 12

Berechnen Sie das Volumen V eines Prismas (Quaders)
mit der Länge a = 2,7 dm, der Breite b = 9,3 cm und 
der Höhe h = 85 mm.    

V =  cm³

Aufgabe 13 Berechnen Sie das Volumen V eines Dreieckprismas mit der Gesamtlänge l = 5,3 cm, der Grundseite des Dreiecks a = 60 mm und der Höhe des Dreiecks h = 1,7 cm.

Aufgabe 14 Berechnen Sie das Volumen V eines rechtwinkligen Dreieckprismas mit der Gesamtlänge l = 5,3 cm und der Länge der Katheten a = 45 mm und b = 2,5 cm. V = dm³

Aufgabe 15 Berechnen Sie die Oberfläche O eines rechtwinkligen Dreieckprismas mit der Gesamtlänge l = 4 cm und der Länge der Katheten a und b = 2,5 cm.

Aufgabe 16 Berechnen Sie das Volumen V des dargestellten Körpers. V = cm³

Aufgabe 17 Berechnen Sie das Volumen V des dargestellten Körpers.

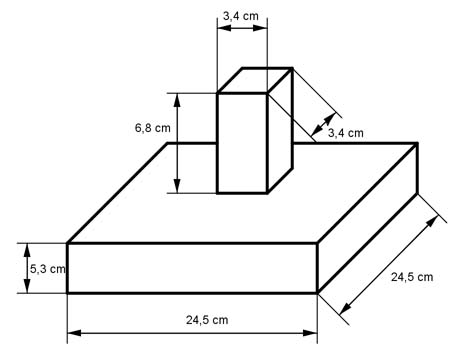
Aufgabe 18 Berechnen Sie das Volumen V des dargestellten Körpers. V = cm³

Aufgabe 19 Berechnen Sie das Volumen V des dargestellten Körpers.

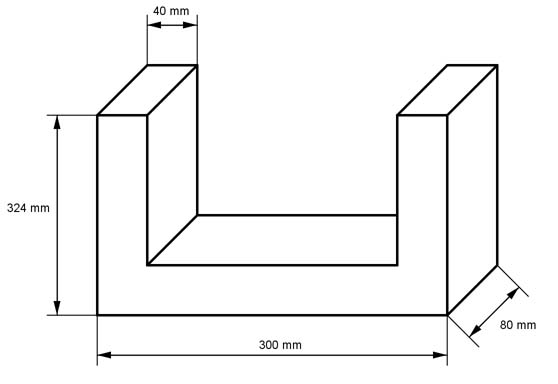
Aufgabe 20 Berechnen Sie das Volumen V des dargestellten Körpers. V = dm³

Aufgabe 21 Berechnen Sie das Volumen V des dargestellten Körpers.

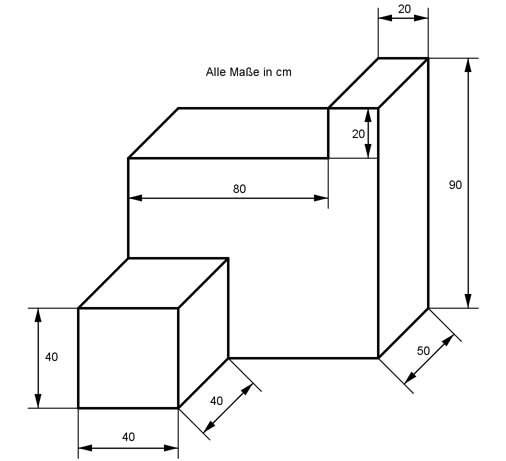
Aufgabe 22 Ein Zylinder hat einen Radius r von 2 m und eine Höhe h von 3 cm. Wie groß ist sein Volumen V? V = cm³

Aufgabe 23 Ein Zylinder hat einen Durchmesser d von 4,8 cm und eine Höhe h von 5 cm. Wie groß ist sein Volumen V?

Aufgabe 24 Ein Zylinder hat einen Grundfläche G von 70 cm² und eine Höhe h von 8 cm. Wie groß ist a) sein Durchmesser d, b) sein Volumen V? d = cm

Aufgabe 25 Berechnen Sie das Volumen V des dargestellten Körpers.

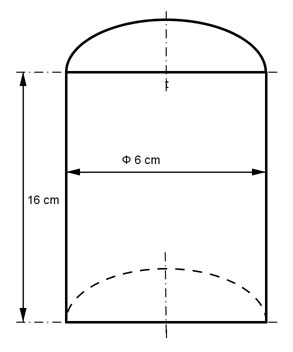
Aufgabe 26 Berechnen Sie das Volumen V des dargestellten Körpers. V = cm³

Aufgabe 27 Berechnen Sie das Volumen V und die Oberfläche O des dargestellten Körpers.

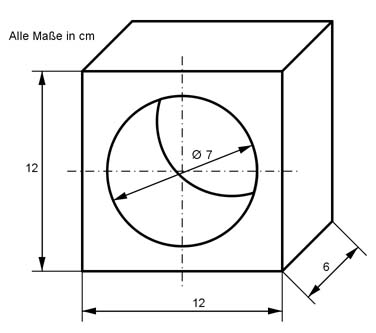
Aufgabe 28 Berechnen Sie das Volumen V des dargestellten Körpers. V = mm³

Aufgabe 29 Berechnen Sie die Oberfläche O eines quadratischen Prismas mit einer Grundfläche G = 25 cm² und einer Länge l von 13 cm.

Aufgabe 30 Ein Würfel hat eine Gesamtseitenlänge L von 72 cm. Wie groß sind sein Volumen V und seine Oberfläche O? V = cm³

Aufgabe 31 Ein Prisma hat eine quadratische Grundfläche mit einem Umfang von 12 cm und einer Höhe von 8 cm. Wie groß sind sein Volumen V und seine Oberfläche O?

Aufgabe 32

Berechnen Sie die Masse m eines Zylinders 
mit r = 2 cm,h = 15 cm und ρ = 7,85 g/cm³.       

m =  g

Aufgabe 33

Berechnen Sie die Masse m eines Zylinders 
mit r = 7,5 cm, h = 65 cm und ρ = 2,7 kg/dm³.

Aufgabe 34

Berechnen Sie die Masse m eines Zylinders 
mit d = 12 mm,h = 27 mm und ρ = 10,5 kg/dm³.         

m =  kg

Aufgabe 35

Berechnen Sie die Masse m eines Zylinders mit 
d = 1,4 m,h = 8,6 m und ρ = 2,4 t/m³.

Aufgabe 36 Ein Zylinder hat ein Volumen V von 200 cm³ und eine Höhe h von 5 cm. Wie groß ist sein Radius r? r = cm

Aufgabe 37 Ein Zylinder hat ein Volumen V von 176 cm³ und einen Radius r von 4,5 cm. Wie groß ist seine Höhe h?

Aufgabe 38 Ein Zylinder hat eine Mantelfläche M von 83,9 cm² und einen Radius r von 3,8 cm. Wie groß sind seine Höhe h und sein Volumen V? h = cm

Aufgabe 39 Ein Zylinder hat eine Mantelfläche M von 246,8 cm² und eine Höhe h von 27 cm. Wie groß sind seine Oberfläche O und sein Volumen V?

Aufgabe 40 Berechnen Sie das Volumen V und die Oberfläche O des dargestellten Körpers. V = mm³

Aufgabe 41 Berechnen Sie das Volumen V und die Oberfläche O des dargestellten Körpers.

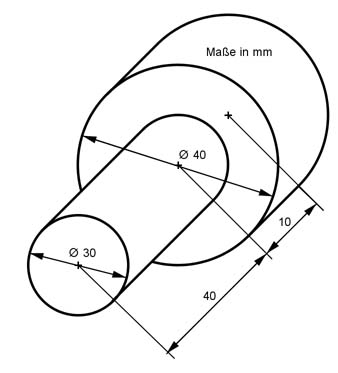
Aufgabe 42 Berechnen Sie die Masse m des Körpers mit einer Dichte ρ von 8,9 g/cm³. m = g

Aufgabe 43 Berechnen Sie die Masse m des Körpers mit einer Dichte ρ von 2,7 kg/dm³.

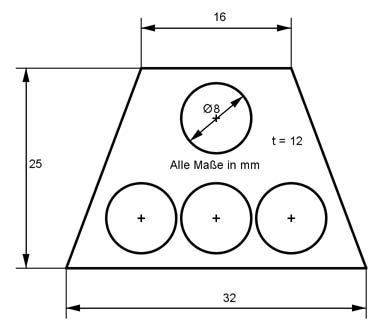
Aufgabe 44 Berechnen Sie die Masse m des Körpers mit einer Dichte ρ von 7,8 g/cm³. m = g

Aufgabe 45 Ein Zylinder hat einen Radius r von 4 cm und eine Höhe h von 6 cm. Wie groß ist seine Oberfläche O?

Aufgabe 46 Ein Zylinder hat ein Volumen V von 17 cm³ und einen Radius r von 2 cm. Wie groß sind seine Oberfläche O und seine Mantelfläche M? M = cm²

Aufgabe 47 Ein Zylinder hat ein Volumen V von 70 cm³ und eine Höhe h von 5 cm. Wie groß sind seine Oberfläche O und seine Mantelfläche M?

Aufgabe 48 Ein Zylinder hat eine Oberfläche O von 91 m² und einen Radius r von 3 m. Wie groß sind seine Mantelfläche M und sein Volumen V? V = m³

Aufgabe 49 Berechnen Sie das Volumen V und die Oberfläche O des dargestellten Körpers.

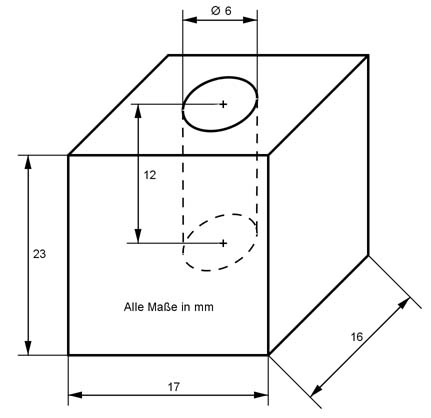
Aufgabe 50 Berechnen Sie das Volumen V und die Oberfläche O des dargestellten Körpers. O = mm²

Aufgabe 51 Berechnen Sie das Volumen V eines Prismas mit einer Höhe h von 5 cm und einem gleichseitigen Dreieck mit einer Seitenlänge a von 4 cm als Grundfläche.

Aufgabe 52 Berechnen Sie das Volumen V eines Prismas mit einer Höhe h von 5 cm und einem regelmäßigen Sechseck mit einer Seitenlänge a von 3 cm als Grundfläche. V = cm³

Aufgabe 53 Berechnen Sie das Volumen V eines Prismas mit einer Höhe h von 5 cm und einem regelmäßigen Achteck mit einer Seitenlänge a von 2,5 cm als Grundfläche.

Aufgabe 54 Berechnen Sie das Volumen V eines Prismas mit einer Höhe h von 5 cm und einem regelmäßigen Fünfeck mit einer Seitenlänge a von 3,2 cm als Grundfläche. V = cm³

Aufgabe 55 Berechnen Sie das Volumen V und die Oberfläche O des dargestellten Prismas.

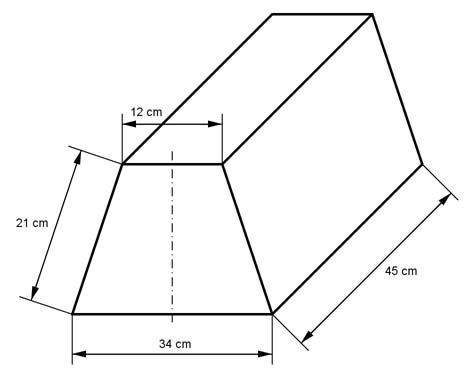
Aufgabe 56 Berechnen Sie das Volumen V und die Oberfläche O des dargestellten Körpers. O = cm²

Aufgabe 57 Ein Zylinder hat einen Umfang U von 46,8 cm und eine Höheh von 12,3 cm. Wie groß sind seine Oberfläche O und seine Mantelfläche M?

Aufgabe 58 Ein Zylinder hat ein Volumen V von 15,7 dm³. Seine Höhe h und der Radius r stehen im Verhältnis 5 : 2. Wie groß sind seine Höhe h und seine Oberfläche O? h = dm

Aufgabe 59 Ein Zylinder hat eine Oberfläche O von 356 cm³. Seine Höhe h und der Radius r stehen im Verhältnis 5 : 3. Wie groß ist sein Volumen V?

Aufgabe 60 Ein Würfel hat eine Masse von 655 g und eine Dichte von 7,85 g/cm³. Wie groß ist eine Seite a? a = cm

Aufgabe 61 Wie groß ist die Masse m des dargestellten Körpers, wenn seine Dichte 7,1 g/cm³ beträgt?

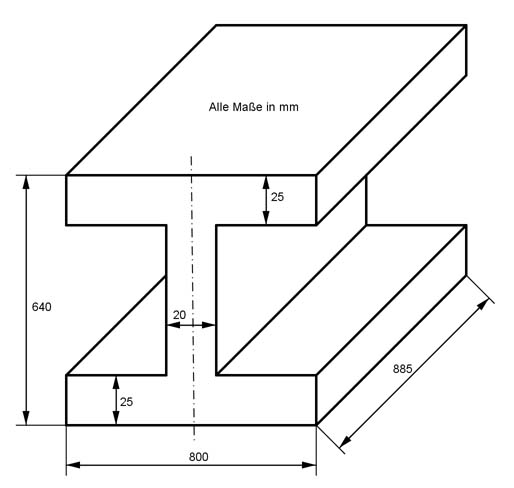
Aufgabe 62 Berechnen Sie das Volumen V und die Oberfläche O des dargestellten symmetrischen Körpers. Alle Maße in mm. O = cm²

Aufgabe 63 Die Seiten eines Rechteckprismas (Quaders) verhalten sichwie a : b : c = 1 : 3 : 5.. Wie groß sind sein Volumen V und seine Oberfläche O, wenn b = 18 cm lang ist?

Aufgabe 64 Ein Quader hat eine Seite mit 5 cm und eine andere mit 2 cm. Wie groß muss die dritte Seite c sein, wenn die Oberfläche des Quaders gleich groß sein soll wie die Oberfläche eines Würfels mit einer Seitenlänge von 5 cm? Sie muss cm lang sein.

Aufgabe 65 Ein quadratisches Prisma hat eine Seite von 36 cm und eine Länge von 62 cm. Ein Rechteckprisma soll gleiches Volumen und gleiche Länge haben. Wie lang ist die andere Rechteckseite, wenn die eine 5,5 cm lang ist?

Aufgabe 66 Rechteckprisma hat die Maße 28 mm x 24 mm x 140 mm. Ein quadratisches Prisma soll gleiches Volumen und gleiche Länge haben. Wie lang ist eine Quadratseite? Sie ist cm lang.

Aufgabe 67 Ein regelmäßiges dreiseitiges Prisma hat eine Oberfläche O von 20 cm² und eine Seitenlänge a von 2 cm. Wie groß ist seine Länge l?

Aufgabe 68 Ein Zylinder hat ein Volumen V von 100 cm³ und eine Höhe h von 5 cm. Wie groß ist sein Durchmesser d? d = cm

Aufgabe 69 Ein Zylinder wird in der Mitte der Länge nach durchgeschnitten. Die Schnittfläche ist ein Quadrat mit der Seite a = 4 cm. Wie groß sind das Volumen V und die Oberfläche O des Zylinders?

Aufgabe 70 Der Radius r und die Höhe h eines Zylinders verhalten sich wie 3 : 5. Wie groß sind das Volumen V und die Mantelfläche M, wenn r = 2 cm? M = cm²

Aufgabe 71 Wie groß ist das Volumen V eines Zylinders, wenn seine Mantelfläche M = 100 cm² und seine Höhe h = 10 cm betragen?

Aufgabe 72 Ein Zylinder hat einen Radius r₁ von 5 cm und eine Höhe h₁ von 8 cm. Er soll einem zweiten volumengleich sein, dessen Radius r₂ und Höhe h₂ sich wie 3 : 5 verhalten. Wie groß sind r₂ und h₂? h₂ = cm

Aufgabe 73 Das Volumen eines Hohlzylinders ist so groß wie sein Innenvolumen. Drücken Sie den Außenradius r₁ durch den Innenradius r₂ aus.

Aufgabe 74 Das Volumen eines Hohlzylinders ist so groß wie sein Innenvolumen. Drücken Sie die Mantelfläche des Hohlzylinders M₁ durch die Mantelfläche innen M₂ aus. M₁ = M₂ * (√2 + )

Aufgabe 75 Ein Hohlzylinder hat ein Volumen V von 20 cm³, eine Mantelfläche M von 40 cm²² und eine Höhe h von 4 cm. Wie groß sind sein Außenradius r₁ und sein Innenradius r₂?

Aufgabe 76 Ein Hohlzylinder hat einen Außenradius r₁ von 3 cm und einen Innenradius r₂₂ von 2 cm. Wie groß ist der Radius r eines Zylinders mit gleichen Volumen und gleicher Höhe? r = cm

Aufgabe 77 Die Radien r₁ und r₂ eines Hohlzylinders verhalten sich wie 4 : 3. Wie groß sind sein Volumen V und die Mantelfläche M, wenn r₁ = 4 cm und die Höhe h = 6 cm?